Semana 1
-El martes 04 no tuvimos clases por feriado de carnaval.
FUNCIONES ANALITICAS
Se dice que una f(z) es analitica en Zo si solo si f es derivable para todo Z de algun disco D|Z-Zo|<R
Propiedades
1. si f(z) es analitica en algun dominio, entonces u y v satisfacen las ecuaciones de Cauchy-Rieman para todo (x,y) del dominio.
2.si u(x,y) v(x,y) y sus primeras derivadas parciales son continuas y ademas cumplen las ECR, f(z) es analítica.
3.sea f(z) analitica en un cierto dominio, entonces u y v son armonicas es decir cumplen:
continuamos con ejercicios en clase para practicar.
Semana 2
empezamos viendo las funciones trascendentes como:
INTEGRACIÓN EN EL PLANO COMPLEJO
se aplican las mismas reglas y propiedades de la integración de funciones reales salvo el caso de funciones que sean eminentemente complejas tales como |Z|, en los cuales se aplican teoremas específicos.
en el caso de integrales indefinidas de funciones analíticas se mantiene la analogía con las reales sin embargo con ciertas diferencias debido a :
i) los números reales se presentan en el eje de las x y las integrales se entienden como una aproximación de la suma de Riemann
ii) los numeros complejos se representan en el plano complejo, lo cual nos lleva a considerar integrales de linea sobre una curva C sobre el plano en lugar de las sumas de Riemann
iii)En las integrales cerradas se presentan propiedades novedosas y que solo se cumplen para las funciones de variable compleja asi como por ejemplo la integral de Cauchy.
INTEGRALES DEFINIDAS
En el caso de que f(z) tenga una autoderivada se puede evaluar la integral definida
donde C es elemento de los complejos y es la constante de integración
CURVAS EN EL PLANO COMPLEJO γ
una curva γ en el plano complejo es el conjunto de puntos (x,y) tal que
INTEGRAL DE LINEA
propiedades
1) si γ es una curva suave a intervalo y f(z) es una funcion continua
si existe
entonces
5) Si  es una curva suave representada por z= z(t), para 0 menor y igual a t y t menor y igual a b y f(z) es continua en c, entonces:
es una curva suave representada por z= z(t), para 0 menor y igual a t y t menor y igual a b y f(z) es continua en c, entonces:
 es una curva suave representada por z= z(t), para 0 menor y igual a t y t menor y igual a b y f(z) es continua en c, entonces:
es una curva suave representada por z= z(t), para 0 menor y igual a t y t menor y igual a b y f(z) es continua en c, entonces:
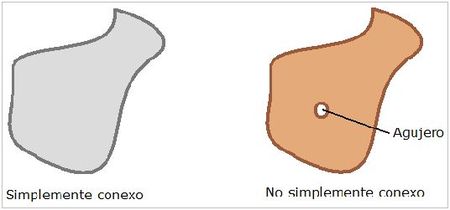
CONJUNTO SIMPLEMENTE CONEXO
D es un dominio simplemente conexo si solamente contiene puntos de D en forma practica seria que no tiene huecos
Propiedad 6
Sea γ una curva suave a intervalos de z1 a z2 en su dominio simplemente CONEXO D si f(z) es analitica en D y sea F'(z)=f(z) en D entonces
Sea γ una curva suave a intervalos de z1 a z2 en su dominio simplemente CONEXO D si f(z) es analitica en D y sea F'(z)=f(z) en D entonces
LONGITUD DE CURVA
si γ se representa por Z=z(t), su longitud en el intervalo a<t<b se calcula
INTEGRALES DE LINEA CERRADAS
la curva suave γ es una curva cerrada
la curva suave γ es una curva cerrada
se presentan los teoremas e integrales de cauchy, como propias de integrales de funciones complejas.
PROPIEDAD 1
TEOREMA DE LA INTEGRAL DE CAUCHY
sea f(z) una funcion analitica en D, un dominio simplemente conexo y γ una curva cerrada simple(sin cruzamientos) entonces se cumple
PROPIEDAD 1
TEOREMA DE LA INTEGRAL DE CAUCHY
sea f(z) una funcion analitica en D, un dominio simplemente conexo y γ una curva cerrada simple(sin cruzamientos) entonces se cumple
PROPIEDAD 2
si f es analitica en un dominio simplemente conexo D, entonces
la integral es independiente de la trayectoria .
siendo γ1 y γ2 so trayectorias diferentes
PROPIEDAD 3
teorema de la deformacion
Sea f una funcion analitica en un dominio D, excepto en z0 y sean curvas cerradas simples que encerran a z0
PROPIEDAD 4
Integral de Cauchy
Si f es analitica en un dominio D simplemente conexo , Sea γ cualquier curva cerrada sim'le en D, que encierre a Zo
PROPIEDAD 5
Formula integral de cauchy para derivadas superiores
si f es analitica en un dominio D simplemente conexo. Sea γ cualquier curva cerrada simple en D, que encierre a Zo














.png)





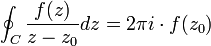

No hay comentarios:
Publicar un comentario