Semana 1
En la primera clase recibimos indicaciones generales de
parte de la Ing. Matilla, las mismas que fueron para la creación de este blog y
cómo será el progreso de la materia durante el presente semestre.
En la segunda clase realizamos una revisión acerca de Los
Números complejos:
Números Complejos
Forma Algebraica
Forma Algebraica
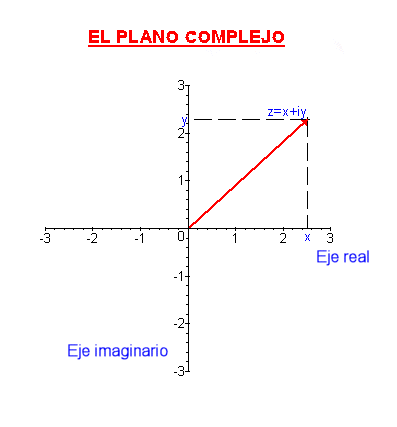
z=x+iy
Parte real R(z)=x
Parte Imaginaria
Im(z)=y
Plano complejo
Observaciones:
·
Si la parte imaginaria es igual a cero,
entonces es un número Real
1. Z.Z = | z | cuadrado
2. | z . w | = | z. w |
3. ang (z.w) = ang z + ang w
4. ang(z/w) = ang z - ang w
- CONJUGADOEl conjugado de un numero complejo se obtiene al cambiar el signo de su componente imaginaria. Por lo tanto, el conjugado de un número complejo
z = x + iyseria :z= x - iyDIVISIÓN DE NÚMEROS COMPLEJOSPara realizar la división se multiplica por el conjugado en el numerador y en el denominador.Si se tiene:z1 = a + ib ^ z2 = c + id
Semana 2
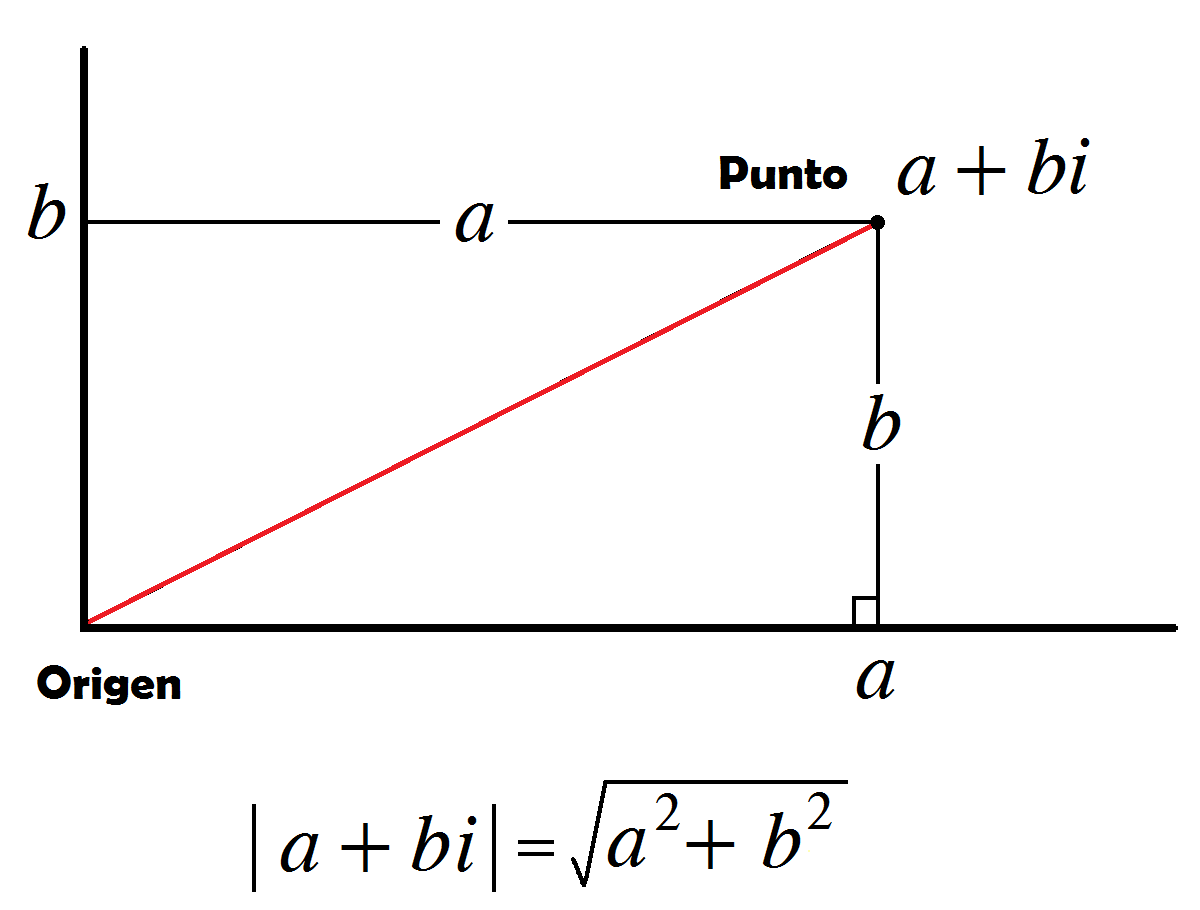
En esta semana empezamos con el módulo de un complejo y su forma trigonométrica
PROPIEDADES
1. Z.
2. | z . w | = | z. w |
3. ang (z.w) = ang z + ang w
4. ang(z/w) = ang z - ang w
5. si W no es cero
entonces |Z/W|=|Z|/|W|
RADICACION
EXPONENCIALES COMPLEJOS
FOTMULA DE EULER
Semana 3
LOGARITMOS EN COMPLEJOS
Valor pricipal
Valor general
se cumplirían las mismas propiedades que en los reales
Semana 4
FUNCIONES DE VARIABLE
- el conjunto de salida y de llegada son los complejos
- para calcular la imagen de z se lo realiza como en las funciones reales
LIMITES
CONTINUIDAD
DERIVADAS





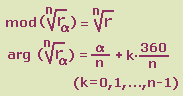
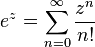









No hay comentarios:
Publicar un comentario